[백준 2579] 계단오르기 파이썬 풀이 - DP
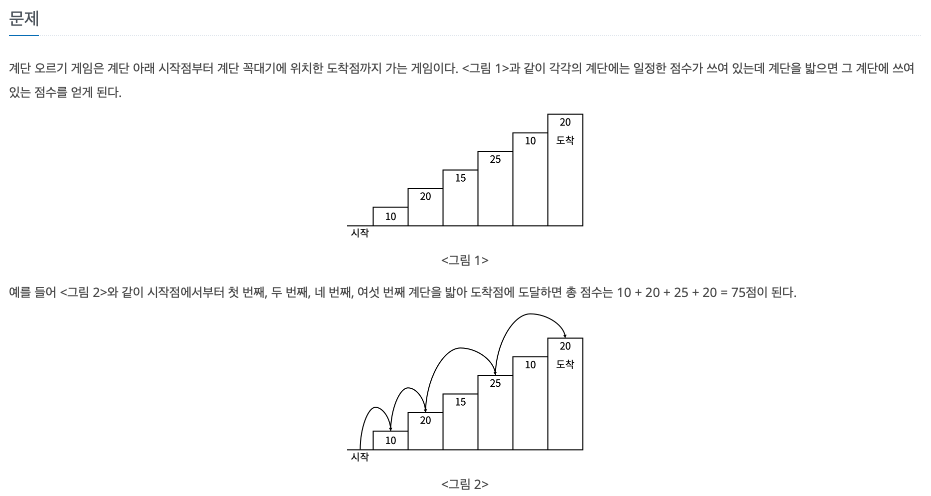
문제
문제 링크 : 백준 2579
규칙은
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
잘못 푼 풀이
처음에 DP문제를 패턴을 분석해서 점화식을 찾으려고 노력했는데 찾은 패턴을 아래와 같다.
연속 세 계단을 밟지 못한다는 규칙 덕분에 나올 수 있는 경우의 수는 적다. 점화식은 찾지 못했는데, 찾은 패턴은 있었다.
- 한 칸을 올라가기 위해서는 직전 계단은 두 칸을 올라가야 한다.
- 두 칸은 직전 계단을 한 칸이든 두 칸이든 상관이 없다. 큰 값을 담으면 된다.
그래서 2차원 배열로 만들어서 모든 경우의 수를 비교해 큰 값을 계속 담아가는 코드를 만들었다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 2579
n = int(input())
result = [[0 for j in range(3)] for i in range(301)]
a = [int(input()) for _ in range(n)]
for i in range(1,n+1):
if i > 1:
# 한 계단을 가기위해 직전 두 계단 올라온 위치에서 더한다.
result[i][1] = result[i-1][2] + a[i-1]
# 두 계단을 가기위해 직전 두 계단이나 직전 한 계단 중 큰 값에서 더한다.
result[i][2] = max(result[i-2][1]+a[i-1], result[i-2][2]+a[i-1])
else :
# 첫번째 계단은 직접 넣어준다.
result[i][1] = a[i-1]
result[i][2] = a[i-1]
print(max(result[n]))
잘못 풀었다고 느낀 이유
- DP문제는 점화식을 찾아야하는데 찾지 못했다.
- 메모리를 낭비하는 풀이이다.
점화식을 우선으로 찾도록 해야하는 것 같다. 그래서 다시 풀어봤다.
다시 푼 풀이
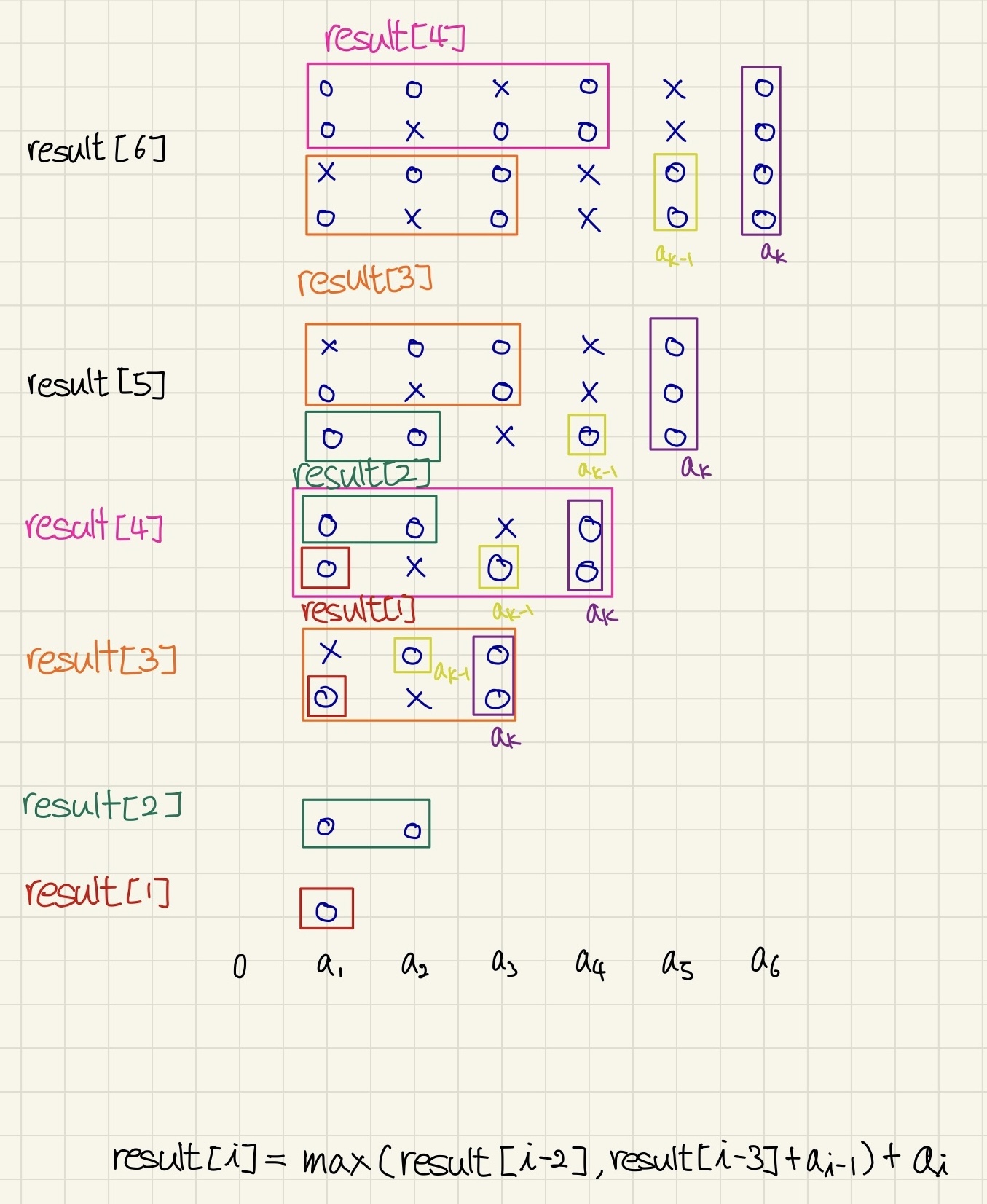
계단을 가는 표현이 아니라 한 구역씩 방문하는 느낌으로 o와 x로 표시했다. 한 계단을 가면 o, 두 계단을 가면 x o 로 표시했다.
그리고 패턴을 찾는다.
잘못 푼 풀이에서 힌트를 많이 받아왔다.
- 두 계단씩 올라가면 큰 값을 가질 수 없다.
- 따라서 항상 식은 한 계단 + 두 계단 or 두 계단 + 한 계단 이동한다.
점화식을 찾을 수 있다!
정답 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 2579
n = int(input())
result = [0 for _ in range(n + 1)]
a = [int(input()) for _ in range(n)]
if n == 1:
print(a[0])
else:
result[1] = a[0]
result[2] = a[0] + a[1]
#점화식
for i in range(3, n + 1):
result[i] = max(result[i - 3] + a[i - 2], result[i - 2]) + a[i - 1]
print(result[n])
느낀점
점화식 찾는 게 정말 쉬운 일이 아닌 것 같다..ㅠ 두 번을 풀어서 거의 완벽에 가깝게 공부한 것 같아서 느낌은 좋다. 마지막 정답코드에서 아쉬운 점은 a의 0번부터 값을 넣어서 보기 어려워 보인다. index 0을 비우고 1부터 값을 넣어야겠다.
정말.. 풀면 풀수록 DP문제는 매력적이야…